Breadth-first Search in AI

 Breadth-first Search

• Breadth-first search is the most common search strategy for traversing a tree or graph. This algorithm searches breadthwise in a tree or graph, so it is called breadth-first search.
• BFS algorithm starts searching from the root node of the tree and expands all successor node at the current level before moving to nodes of next level.
• The breadth-first search algorithm is an example of a general-graph search algorithm.
• Breadth-first search implemented using FIFO queue data structure.

Advantages:

• BFS will provide a solution if any solution exists.
• If there are more than one solutions for a given problem, then BFS will provide the minimal solution which requires the least number of steps.

Disadvantages:

• It requires lots of memory since each level of the tree must be saved into memory to expand the next level.
• BFS needs lots of time if the solution is far away from the root node.

Example:

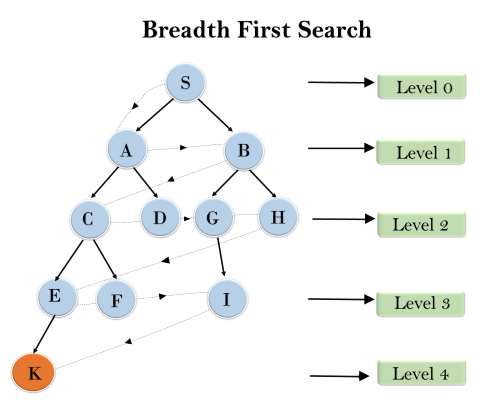
In the below tree structure, we have shown the traversing of the tree using BFS algorithm from the root node S to goal node K. BFS search algorithm traverse in layers, so it will follow the path which is shown by the dotted arrow, and the traversed path will be:

1. S---> A--->B---->C--->D---->G--->H--->E---->F---->I---->K  

Time Complexity: Time Complexity of BFS algorithm can be obtained by the number of nodes traversed in BFS until the shallowest Node. Where the d= depth of shallowest solution and b is a node at every state.

T (b) = 1+b²+b³+.......+ b^d= O (b^d)

Space Complexity: Space complexity of BFS algorithm is given by the Memory size of frontier which is O(b^d).

Completeness: BFS is complete, which means if the shallowest goal node is at some finite depth, then BFS will find a solution.

Optimality: BFS is optimal if path cost is a non-decreasing function of the depth of the node.