Bidirectional, Iterative deepeningdepth-first, Uniform-cost, Depth-Limited Search Algorithm

 1. Depth-Limited Search Algorithm:

A depth-limited search algorithm is similar to depth-first search with a predetermined limit. Depth-limited search can solve the drawback of the infinite path in the Depth-first search. In this algorithm, the node at the depth limit will treat as it has no successor nodes further.

Depth-limited search can be terminated with two Conditions of failure:

• Standard failure value: It indicates that problem does not have any solution.
• Cutoff failure value: It defines no solution for the problem within a given depth limit.

Advantages:

Depth-limited search is Memory efficient.

Disadvantages:

• Depth-limited search also has a disadvantage of incompleteness.
• It may not be optimal if the problem has more than one solution.

Example:

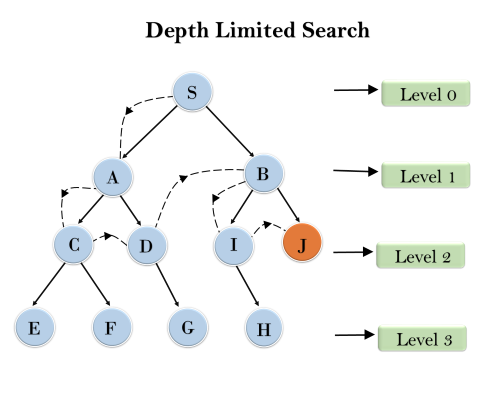
Completeness: DLS search algorithm is complete if the solution is above the depth-limit.

Time Complexity: Time complexity of DLS algorithm is O(b^ℓ).

Space Complexity: Space complexity of DLS algorithm is O(b×ℓ).

Optimal: Depth-limited search can be viewed as a special case of DFS, and it is also not optimal even if ℓ>d.

2. Uniform-cost Search Algorithm:

Uniform-cost search is a searching algorithm used for traversing a weighted tree or graph. This algorithm comes into play when a different cost is available for each edge. The primary goal of the uniform-cost search is to find a path to the goal node which has the lowest cumulative cost. Uniform-cost search expands nodes according to their path costs form the root node. It can be used to solve any graph/tree where the optimal cost is in demand. A uniform-cost search algorithm is implemented by the priority queue. It gives maximum priority to the lowest cumulative cost. Uniform cost search is equivalent to BFS algorithm if the path cost of all edges is the same.

Advantages:

• Uniform cost search is optimal because at every state the path with the least cost is chosen.

Disadvantages:

• It does not care about the number of steps involve in searching and only concerned about path cost. Due to which this algorithm may be stuck in an infinite loop.

Example:

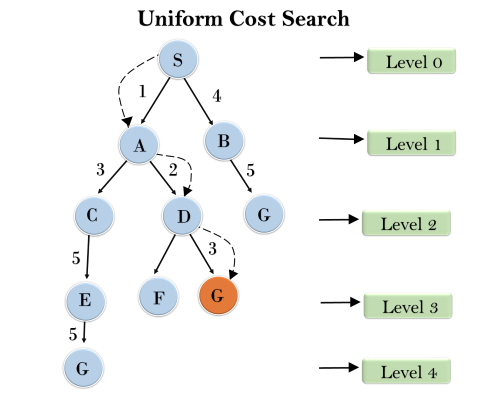
Completeness:

Uniform-cost search is complete, such as if there is a solution, UCS will find it.

Time Complexity:

Let C* is Cost of the optimal solution, and ε is each step to get closer to the goal node. Then the number of steps is = C*/ε+1. Here we have taken +1, as we start from state 0 and end to C*/ε.

Hence, the worst-case time complexity of Uniform-cost search isO(b^{1 + [C*/ε]})/.

Space Complexity:

The same logic is for space complexity so, the worst-case space complexity of Uniform-cost search is O(b^{1 + [C*/ε]}).

Optimal:

Uniform-cost search is always optimal as it only selects a path with the lowest path cost.

3. Iterative deepeningdepth-first Search:

The iterative deepening algorithm is a combination of DFS and BFS algorithms. This search algorithm finds out the best depth limit and does it by gradually increasing the limit until a goal is found.

This algorithm performs depth-first search up to a certain "depth limit", and it keeps increasing the depth limit after each iteration until the goal node is found.

This Search algorithm combines the benefits of Breadth-first search's fast search and depth-first search's memory efficiency.

The iterative search algorithm is useful uninformed search when search space is large, and depth of goal node is unknown.

Advantages:

• Itcombines the benefits of BFS and DFS search algorithm in terms of fast search and memory efficiency.

Disadvantages:

• The main drawback of IDDFS is that it repeats all the work of the previous phase.

Example:

Following tree structure is showing the iterative deepening depth-first search. IDDFS algorithm performs various iterations until it does not find the goal node. The iteration performed by the algorithm is given as:

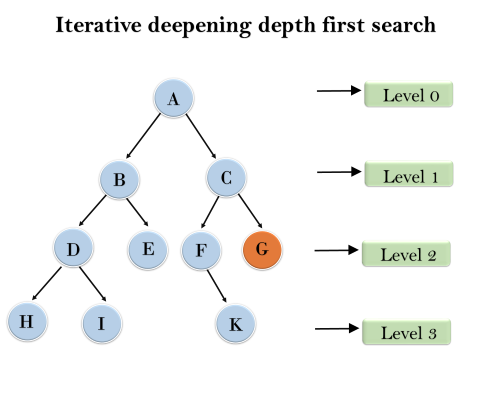
1'st Iteration-----> A
2'nd Iteration----> A, B, C
3'rd Iteration------>A, B, D, E, C, F, G
4'th Iteration------>A, B, D, H, I, E, C, F, K, G
In the fourth iteration, the algorithm will find the goal node.

Completeness:

This algorithm is complete is ifthe branching factor is finite.

Time Complexity:

Let's suppose b is the branching factor and depth is d then the worst-case time complexity is O(b^d).

Space Complexity:

The space complexity of IDDFS will be O(bd).

Optimal:

IDDFS algorithm is optimal if path cost is a non- decreasing function of the depth of the node.

4. Bidirectional Search Algorithm:

Bidirectional search algorithm runs two simultaneous searches, one form initial state called as forward-search and other from goal node called as backward-search, to find the goal node. Bidirectional search replaces one single search graph with two small subgraphs in which one starts the search from an initial vertex and other starts from goal vertex. The search stops when these two graphs intersect each other.

Bidirectional search can use search techniques such as BFS, DFS, DLS, etc.

Advantages:

• Bidirectional search is fast.
• Bidirectional search requires less memory

Disadvantages:

• Implementation of the bidirectional search tree is difficult.
• In bidirectional search, one should know the goal state in advance.

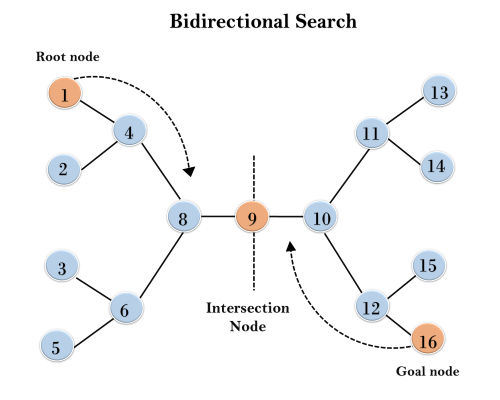
Example:

In the below search tree, bidirectional search algorithm is applied. This algorithm divides one graph/tree into two sub-graphs. It starts traversing from node 1 in the forward direction and starts from goal node 16 in the backward direction.

The algorithm terminates at node 9 where two searches meet.

Completeness: Bidirectional Search is complete if we use BFS in both searches.

Time Complexity: Time complexity of bidirectional search using BFS is O(b^d).

Space Complexity: Space complexity of bidirectional search is O(b^d).

Optimal: Bidirectional search is Optimal.