Depth-first Search in AI

 Depth-first Search

• Depth-first search isa recursive algorithm for traversing a tree or graph data structure.
• It is called the depth-first search because it starts from the root node and follows each path to its greatest depth node before moving to the next path.
• DFS uses a stack data structure for its implementation.
• The process of the DFS algorithm is similar to the BFS algorithm.

Note: Backtracking is an algorithm technique for finding all possible solutions using recursion.

Advantage:

• DFS requires very less memory as it only needs to store a stack of the nodes on the path from root node to the current node.
• It takes less time to reach to the goal node than BFS algorithm (if it traverses in the right path).

Disadvantage:

• There is the possibility that many states keep re-occurring, and there is no guarantee of finding the solution.
• DFS algorithm goes for deep down searching and sometime it may go to the infinite loop.

Example:

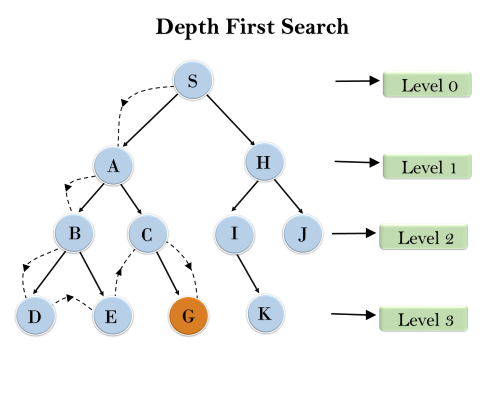
In the below search tree, we have shown the flow of depth-first search, and it will follow the order as:

Root node--->Left node ----> right node.

It will start searching from root node S, and traverse A, then B, then D and E, after traversing E, it will backtrack the tree as E has no other successor and still goal node is not found. After backtracking it will traverse node C and then G, and here it will terminate as it found goal node.

Completeness: DFS search algorithm is complete within finite state space as it will expand every node within a limited search tree.

Time Complexity: Time complexity of DFS will be equivalent to the node traversed by the algorithm. It is given by:

T(n)= 1+ n²+ n³ +.........+ n^m=O(n^m)

Where, m= maximum depth of any node and this can be much larger than d (Shallowest solution depth)

Space Complexity: DFS algorithm needs to store only single path from the root node, hence space complexity of DFS is equivalent to the size of the fringe set, which is O(bm).

Optimal: DFS search algorithm is non-optimal, as it may generate a large number of steps or high cost to reach to the goal node.